Matematica

• 2 Comments

•

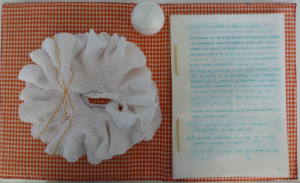
Con grande emozione pubblico queste foto riguardanti la premiazione, il prezioso testo con cui hanno motivato la segnalazione e il mio lavoro:

 

premiazione

P1020514-redim1024

 

Queste le parole con cui hanno motivato la segnalazione di merito:

Ci sono nobilissimi precedenti di libri divorati "per" e "con" ira, o per salvarsi la pelle e, ancora, per amore, ma sostanziosi pasti di teoremi, con le relative dimostrazioni, mancavano: ora la tavola è al completo. Si proceda con gli antipasti.
Avanti le tabelline da masticare, le grammatiche da ingoiare e noi a godere.

Ho intitolato il lavoro: 'Geometrie, un assaggio', si tratta di una breve panoramica sul V postulato di Euclide e la nascita delle geometrie non euclidee scritta su carta edibile con un inchiostro per alimenti e quindi commestibile. L'idea è quella di proporre un argomento di matematica in modo ironico, per sdrammatizzare una materia ostica a molti.
Riporto qui le note per il lettore:

Se la lettura non bastasse a interiorizzare gli argomenti esposti c'è la possibilità di mangiarseli, infatti:

  • la carta e l'inchiostro sono edibili
  • la copertina può essere usata come tovaglietta da pic nic
  • il fermo è uno stuzzicadenti
  • il piano iperbolico all'uncinetto può fungere da tovagliolo

e se la digestione risultasse lenta si può smaltire il tutto giocando a palla con il piano ellittico.

Al seguente link si può scaricare il pdf della scansione di tutto l'articolo Geometrie, un assaggio

•

Il 12 dicembre ci sarà l'apertura della XXI edizione di Libri mai mai visti dove sarà esposto anche un mio lavoro dal titolo: "Geometrie, un assaggio".
Sono molto felice che al mio libro sia stata assegnata una segnalazione di merito perché mi rappresenta molto: un breve testo di matematica sulle geometrie euclidea, ellittica, iperbolica, su un supporto realizzato a mano e il tutto condito con molta ironia. A inaugurazione avvenuta posterò foto e testo.

•

Quando si vuol rimproverare con utilità, e mostrare ad un altro che s'inganna, bisogna osservare da qual verso egli considera la cosa, perché generalmente da quel verso lì essa è giusta, e riconoscergli questa verità, ma svelargli quell'altro verso da cui essa è falsa. Ed egli si contenta di ciò, perché vede che non s'ingannava e che il suo difetto era soltanto di non veder tutti i lati della questione; già, non ci sicruccia di non veder tutto, ma non si vuole ammettere di essersi ingannati; e forse ciò deriva dal fatto che naturalmente l'uomo non può vedere tutto e che naturalmente non può ingannarsi in quel lato che egli considera particolarmente; così come si suol dire che le apprensioni dei sensi son sempre vere.

• 1 Comment

•

Dopo il nastro di Moebius, nella scala delle superfici più famose, c'è la bottiglia di Klein, così ho pensato di realizzarla all'uncinetto:

bottiglia di Klein

Quando l'ho fatta vedere a degli amici mi han fatto notare che sembrava una borsetta, quindi mi son detta che usando del cotone luminoso e facendola un po' più panciuta avrei potuto avere una bella pochette:

Per chi vuole approfondire l'argomento dal punto di vista matematico può leggere questo articolo di Konrad Polthier ricco di immagini e di rimandi.